今天我們要來介紹經典的排序演算法，我還記得我大學的時候，被排序演算法搞的一頭霧水，現在再回去看會覺得：「我以前怎麼那麼笨呀。」不過我相信各位讀者，絕對都是比我還要聰明好幾倍的人，所以我們廢話不多說，開始今天的主題吧！

甚麼是排序？

排序的意思就是，這組數列(也不一定是數列，但要是有順序性的東西，譬如英文字母也可以)，從頭到尾數過去他會是遞增或是遞減，當然也可以有重複的值，但他們會排在隔壁。

講完了上面的廢話後，想跟大家說，排序的演算法有非常多種，時間複雜度最好的是O(n logn)，沒錯！你沒有聽錯，在前人努力的淚水和汗水中，目前為止排序演算法最好的時間複雜度是O(n logn)。
當然不只有O(n logn)的排序演算法，也有O(n^2)的排序演算法，這兩種時間複雜度的排序演算法都各有很多種，譬如O(n^2)的有bubble sort, insertion sort, selection sort等等，O(n logn)的有Quick Sort, Merge Sort, HeapSort等等，今天我會各挑一種來跟大家介紹，其他的大家有興趣可以上網查看看喔！

O(n^2) Sorting Algorithm - Selection Sort

首先我們來看看Selection Sort，其實這個演算法的想法超級簡單的，我們來從頭想起。
想像今天我們有一堆數字積木從1到10，我們把他打亂以後，想要把他從小到大排序，我們會怎麼做？
這很簡單嘛！我會先再數字積木裡找到1然後放在頭，然後繼續在數字積木裡找2放在1後面，然後一直持續一直到把1到10排出來。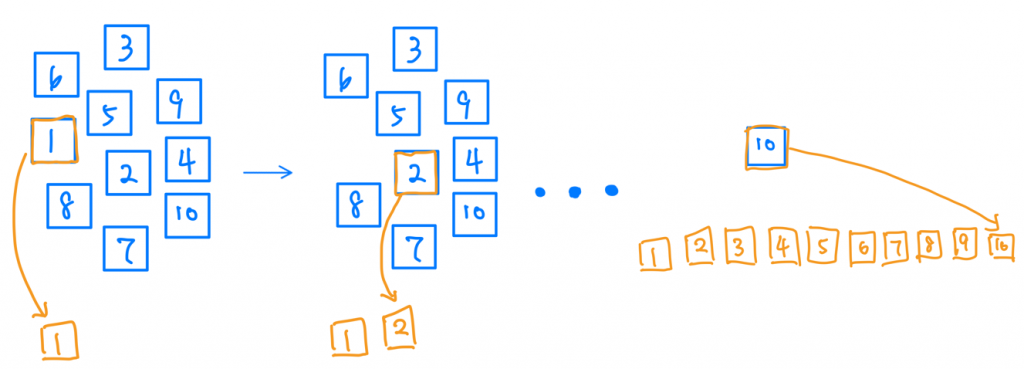

好了我們學完Selection Sort了！
哈哈！這其實就是Selection Sort的精隨，我每次找最小的，把他放到已經排好得那群數字旁邊，僅此而已喔。
另外我們在實作上，如果要用上面的思考邏輯去撰寫，我們勢必要再多宣告一個Array會浪費一點空間，所以我們會改用交換元素的方式來去實作喔。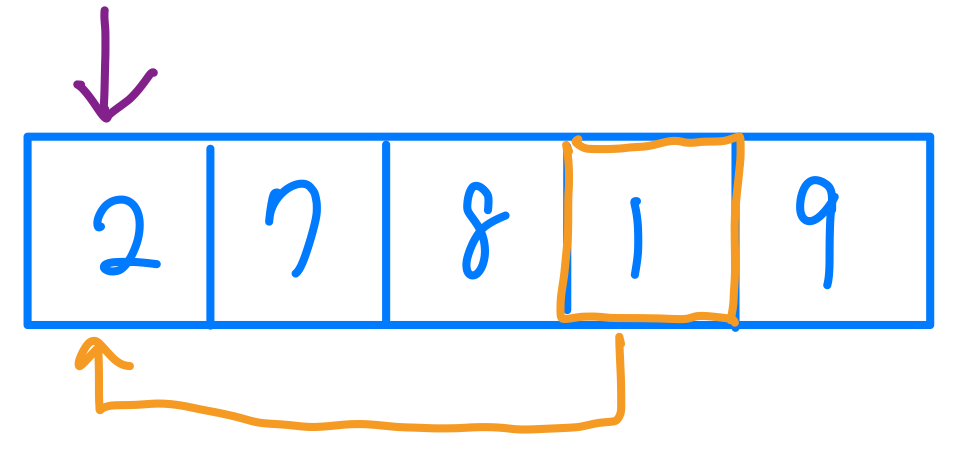

以上圖為例，我找到最小的1之後，就把他跟第一個index裡的值做交換。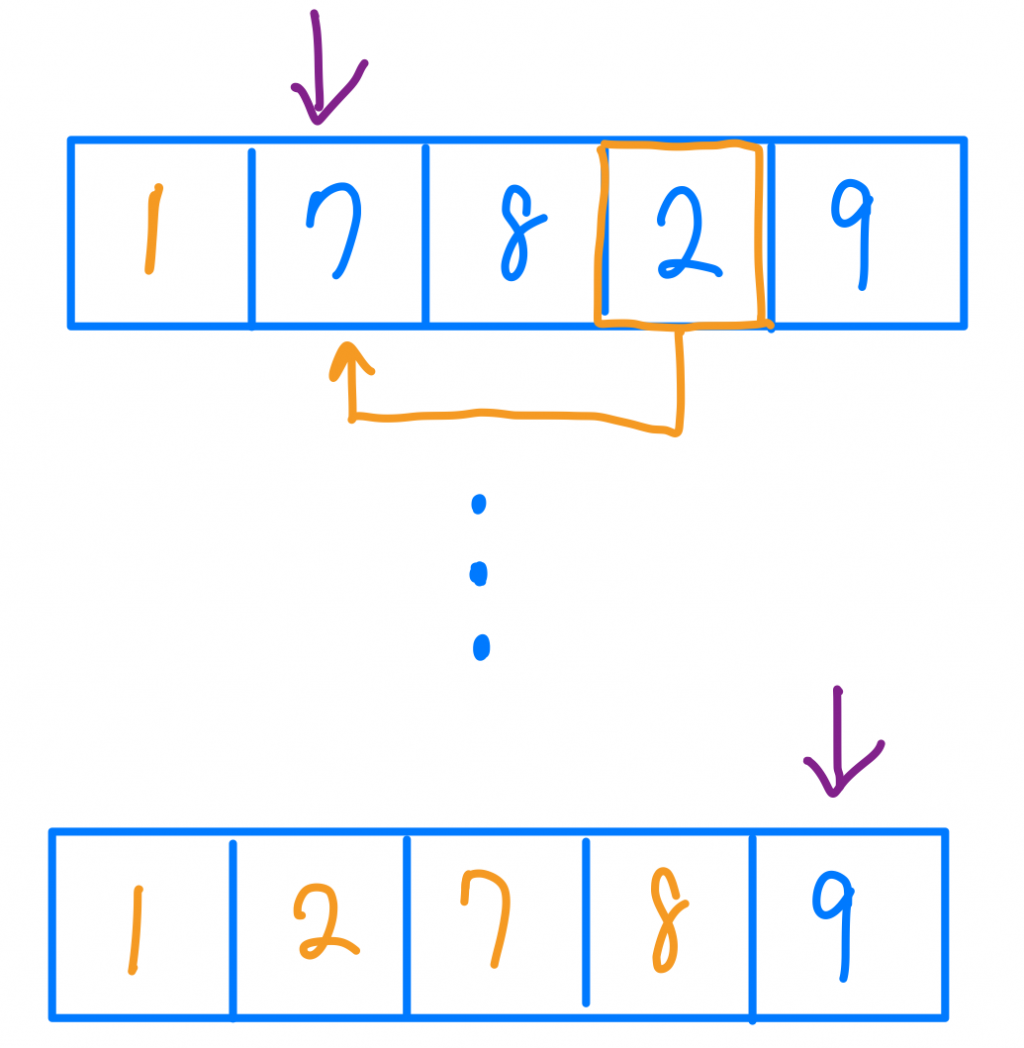

一值重複做到最後一個index就代表排序完成拉。

接下來我們想想如何計算時間複雜度呢？
我們可以把步驟拆解成以下幾個：

1. 從數組中找到最小的
2. 放到排好得那群數字旁邊
3. 重複1到2
   第一個步驟，需要O(n)的時間，n是array的大小，第二個步驟就放過去而已，所以是O(1)，那我們會重複1到2幾次呢？答案是重複n次，所以我時間複雜度總共是O(n^2)。

O(n logn) Sorting Algorithm - Merge Sort

Merge Sort 的方法是這樣，假設我有兩個都已經排序好的Array，我可以在O(2n) 或者可以說O(n)的時間複雜度內將兩個Array合併成一個以排序好的Array。
具體作法是，我分別有兩個指標指向兩個Array，哪一個比較小就把它的值抓出來，然後把指標往後移，一直持續。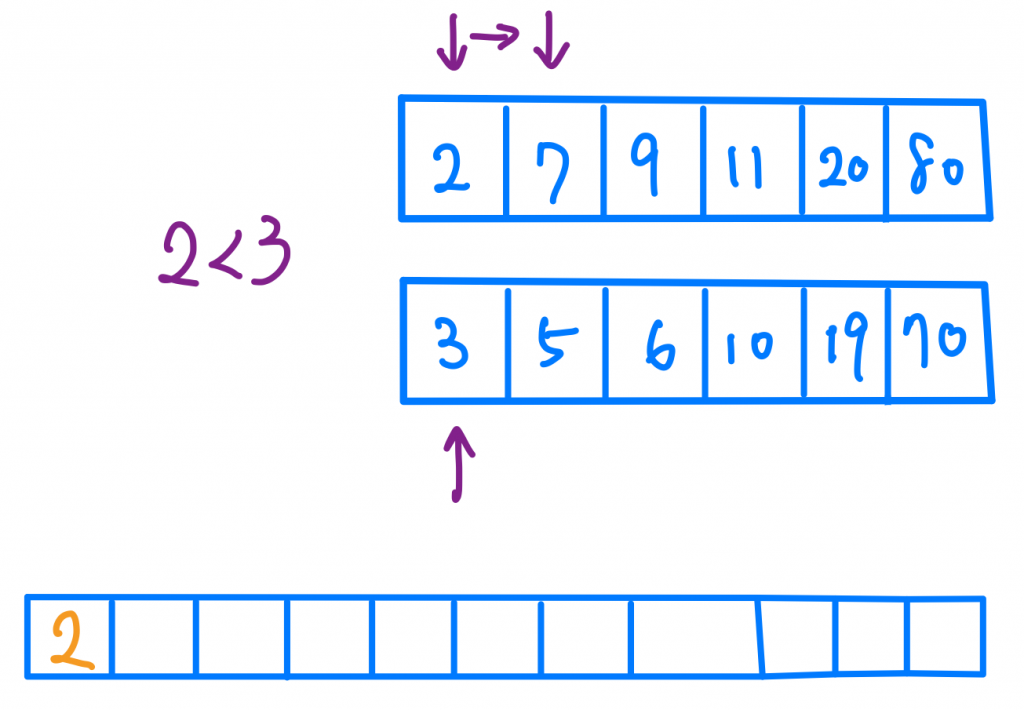


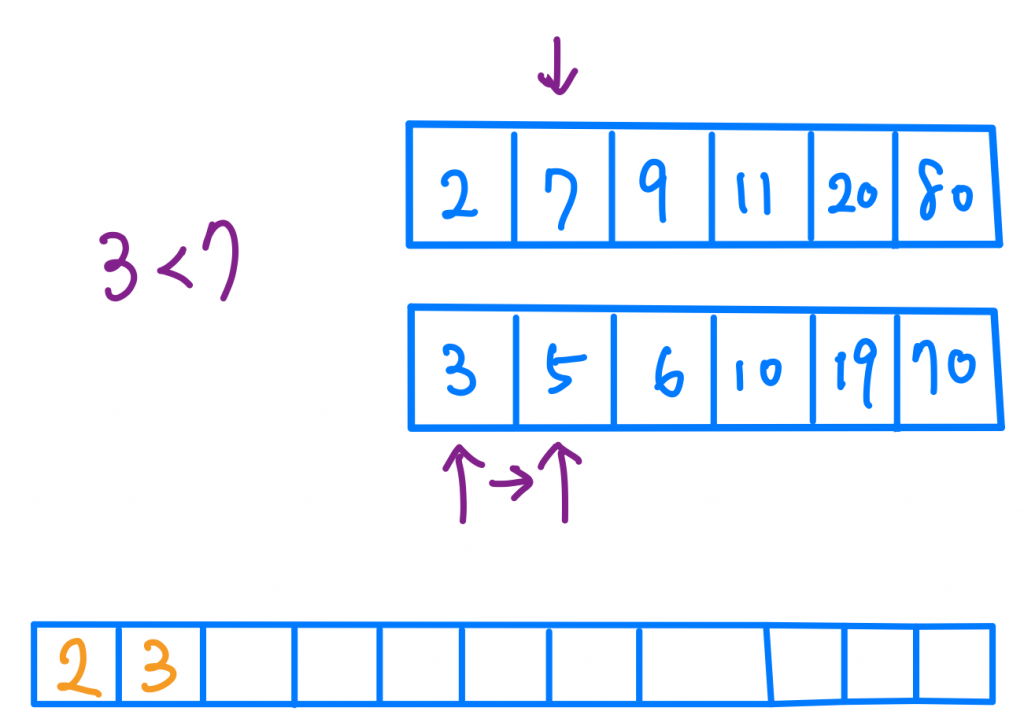
最後就會得到一個完全排序好兩個Array的大Array了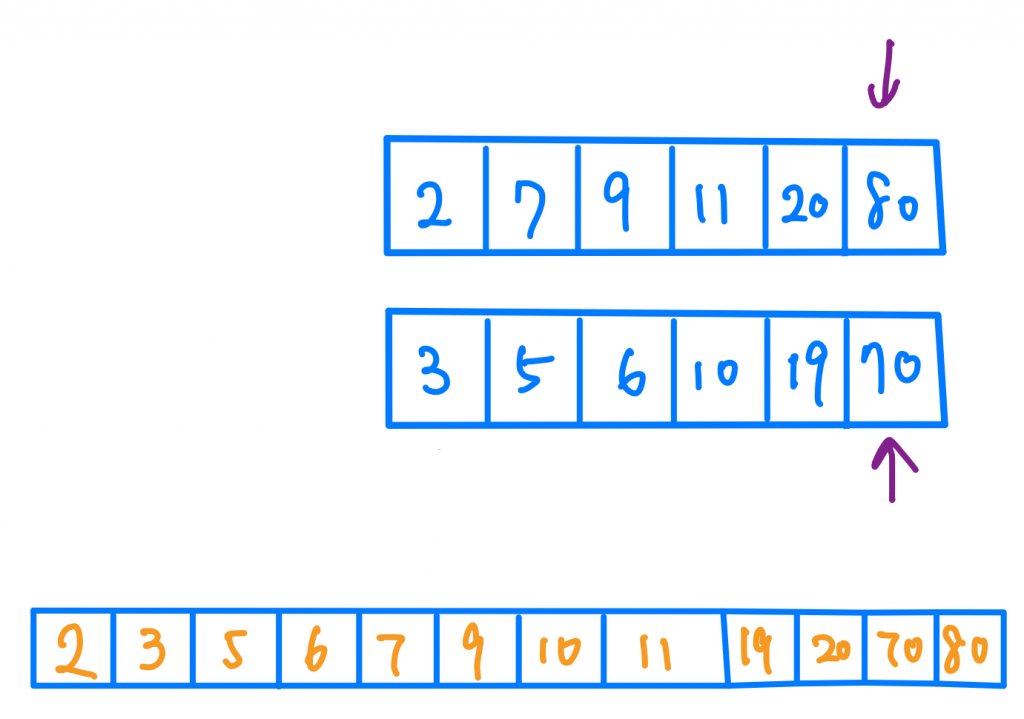

這時候你可能就會說，不對啊！我們的初始條件又不是兩個已經排序好的Array，說這個要幹嘛？！確實確實，現在讓我展現魔法的威力給你看！我們拿其中一個排序好的Array來看，我是不是可以說，他是兩個更短而且排序好的Array在他的O(n)裡面完成合併的呢？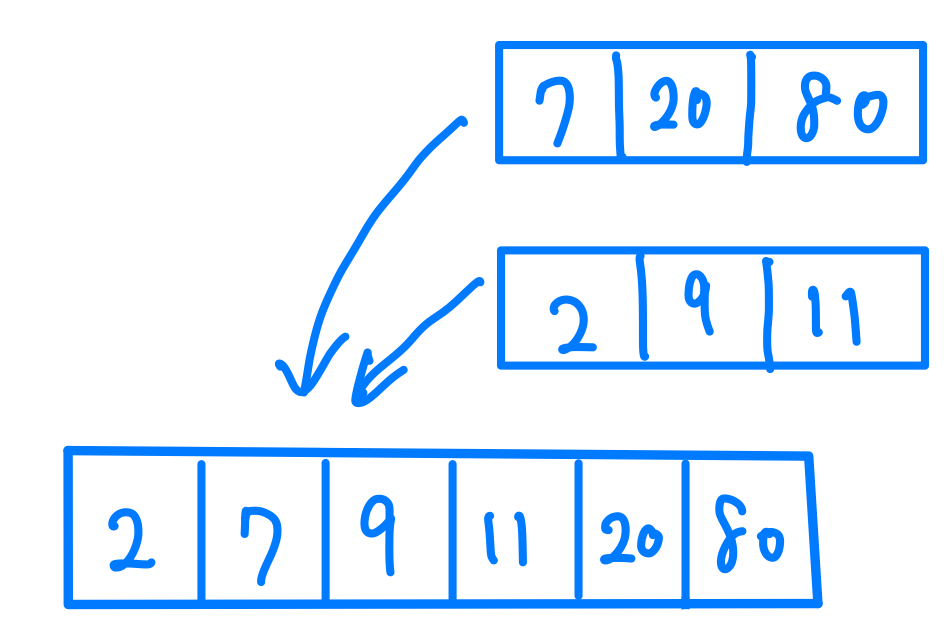

那如果我們在取這兩個更短的Array的其中一個，然後他是不是又是兩個又更短的Array合併完成的呢？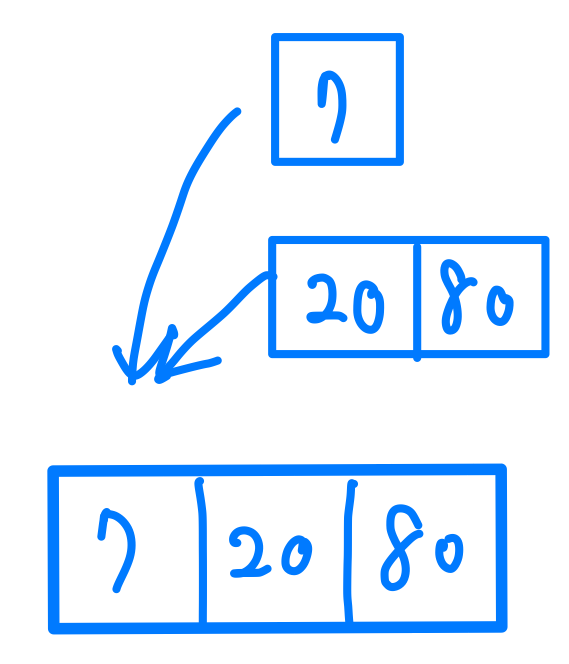

當我們不斷重複以上思想我們會發現，到最後最短的Array其實就是一個元素本身，所以反過來說，如果我們能把元素拆成一個一個，那我就可以用上面提到的合併方式，在組成一個已經排序好的Array，這就是Merge Sort的核心。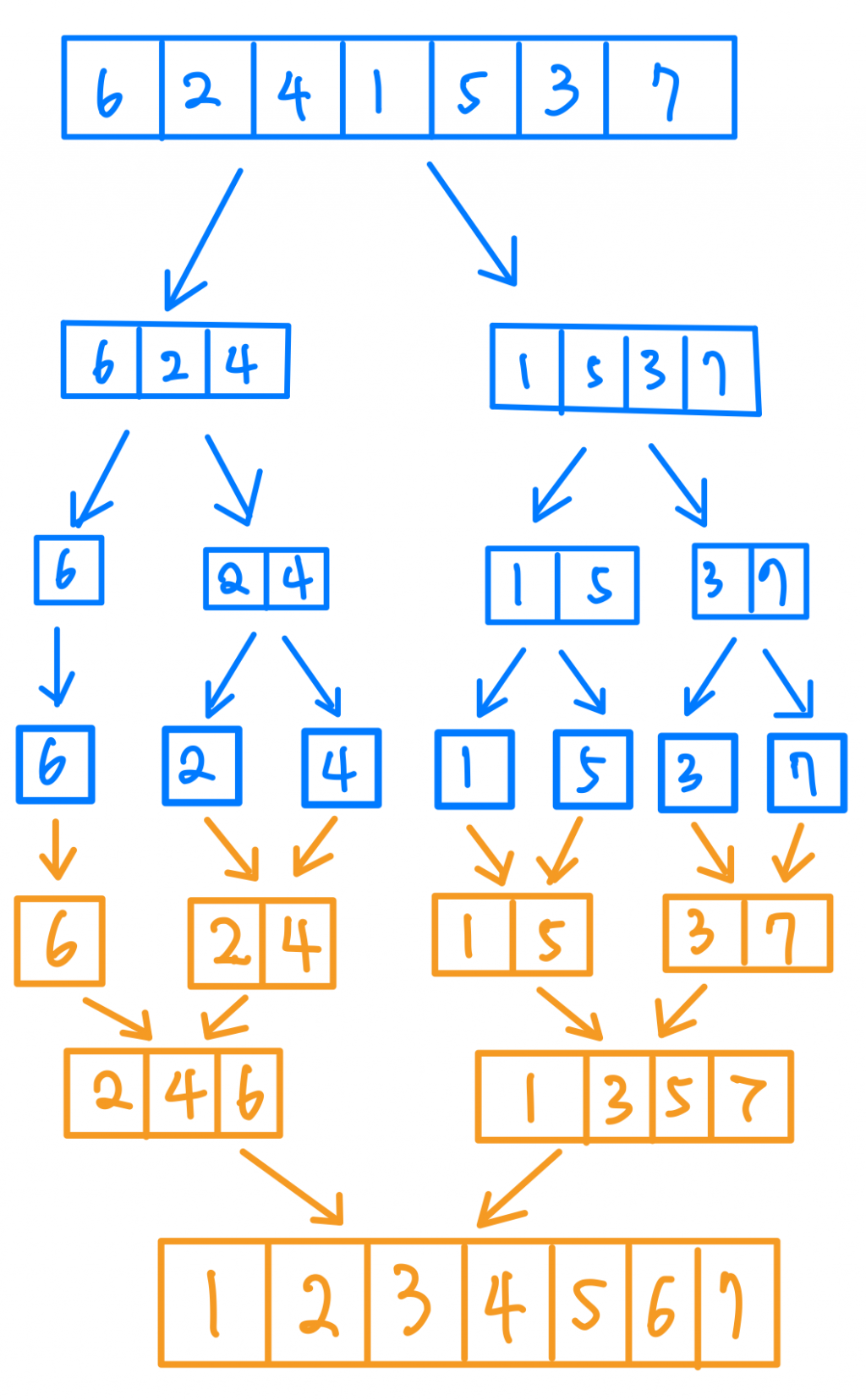

現在我們來把Merge Sort的步驟寫下來

1. 把Array 分成一半，左Array跟右Array
2. 把步驟1的左右子Array拆到只剩一個元素
3. 在O(n)的時間內把左右子Array合併
4. 一直持續步驟3直到結束

這個時間複雜度要怎麼計算呢？先看看步驟1跟2我們總共會拆幾次呢？還記得嗎，一次少一半的就像Binary Search，會拆logn 次，那步驟3跟步驟4呢？因為我們拆幾次就要合併幾次，所以我們要持續做步驟3做logn次，每一次合併都要花O(n)的時間，所以時間複雜度就是O(n logn)。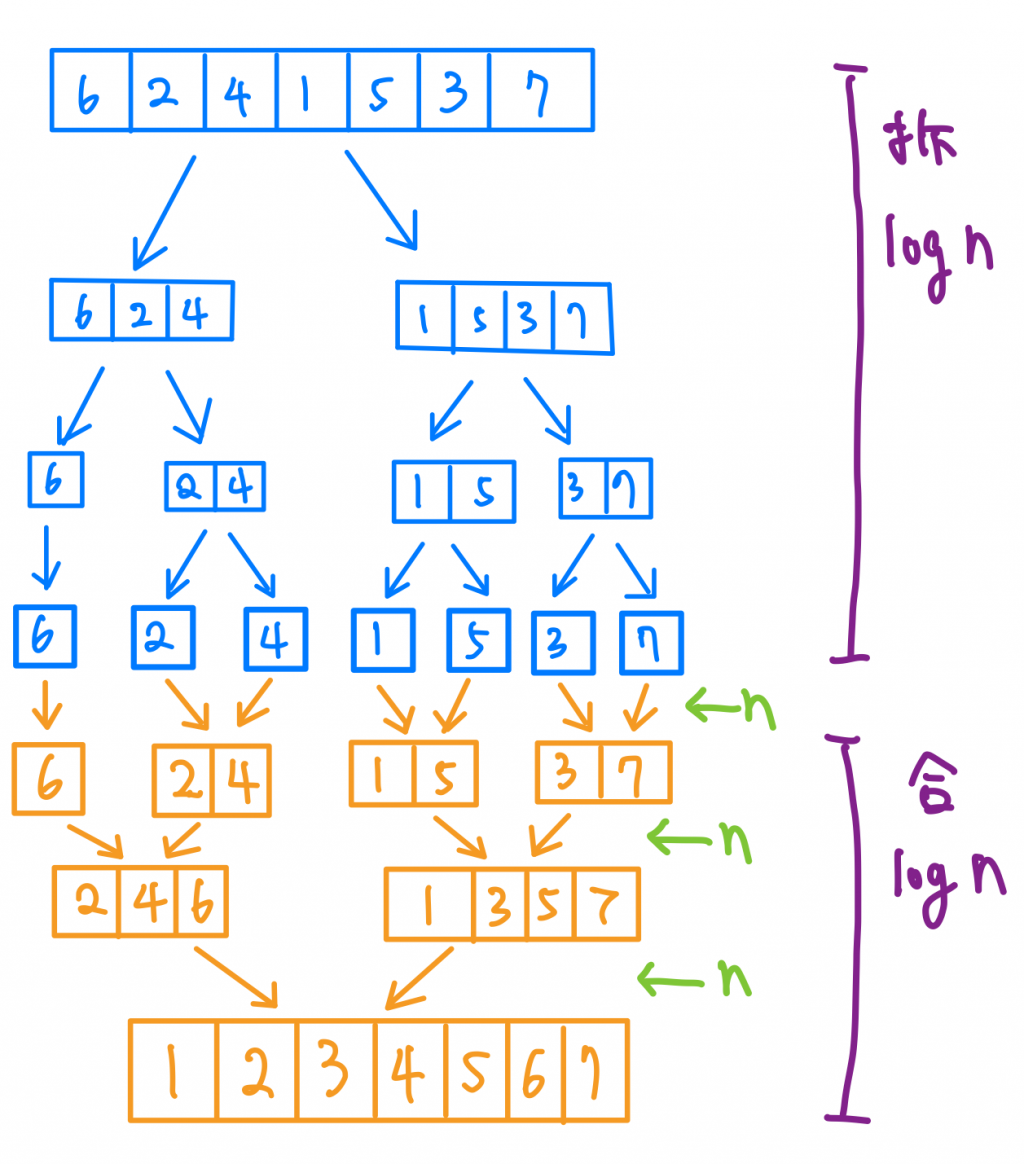

總結

今天跟大家介紹完排序演算法，在這邊要跟各位讀者說，很多程式語言都有內建的Sorting函式庫，通常我們去調用的時候他的時間複雜度是O(n log n)，所以其實以後我們的函式內有需要用到排序時，我們對於那個排序演算法會以O(n log n)的時間複雜度來介紹喔！